こんにちは！
JR静岡駅徒歩3分の中学生専門教室の個別学習Roots.（ルーツ）です。
このコラムでは、2025年度の静岡県公立高校入試問題の数学の解説を行います。
このような方は必見です！
- 2025年度に受験生になる新中学3年生
- 受験勉強のやり方が分からない中学生
- 過去問演習を行なっている受験生
また、個別学習Roots.では、個別の勉強相談を随時承っております。
ご興味のある方は、お気軽にお問い合わせください。
大問7 図形の証明
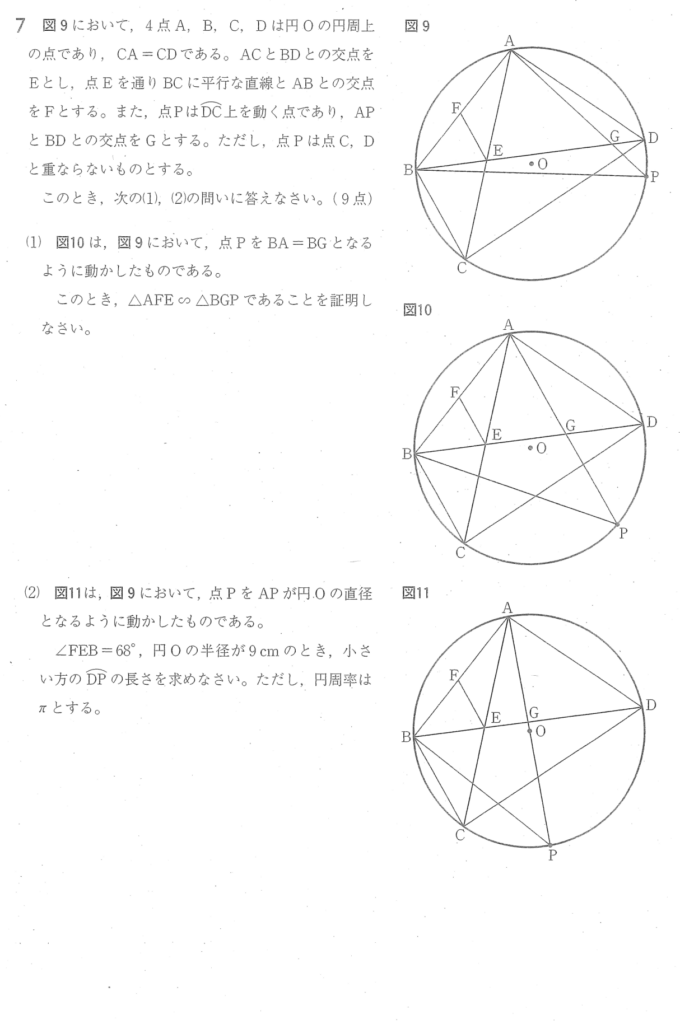
(1) 相似な三角形の証明
△AFEと△BGPにおいて
FE//BCより同位角は等しいので
∠AEF = ∠ACB ・・・①
弧ABの円周角より
∠BPG = ∠ACB ・・・②
①,②より
∠AEF = ∠BPG ・・・③
仮定より
CA = CD ・・・④
BA = BG ・・・⑤
④より△CADは二等辺三角形であり底角は等しいので
∠CAP = CDA ・・・⑥
⑤より△BAGは二等辺三角形であり底角は等しいので
∠BAG = ∠BGA ・・・⑦
弧ADの円周角より
∠ABG = ∠ABD ・・・⑧
⑥,⑦,⑧より△CADと△BAGは頂角が等しい二等辺三角形なので
∠BAG = ∠CAD ・・・⑨
弧PDの円周角より
∠PBG = ∠PAD ・・・⑩
また
∠EAF = ∠BAG – ∠CAP ・・・⑪
∠PAD = ∠CAD – ∠CAP ・・・⑫
⑨,⑪,⑫より
∠PAD = ∠EAF ・・・⑬
⑩,⑬より
∠EAF = ∠PBG ・・・⑭
③,⑭より、2組の角がそれぞれ等しいので、
△AFE ≡ △BGP
(1)の配点
配点 6点
(2) 弧の長さ
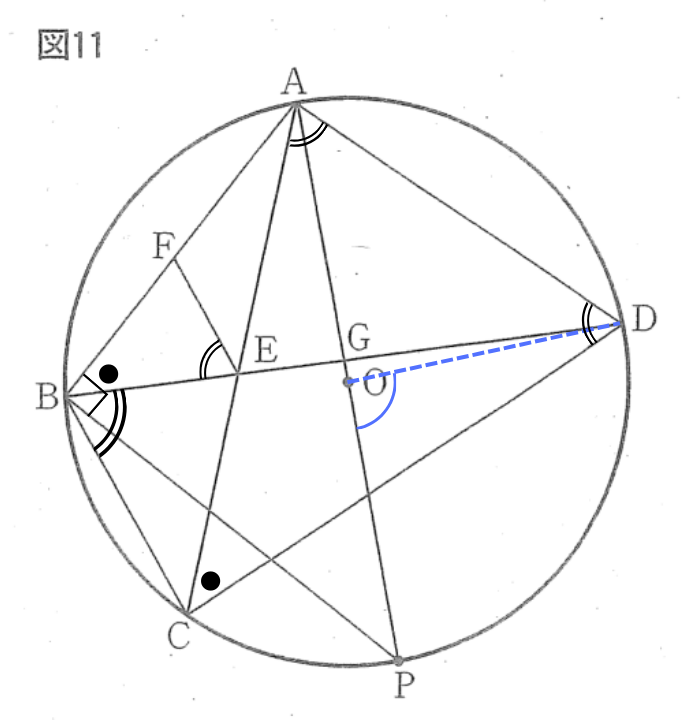
上図のように、補助線として線分ODを引く。
FE//BCより、錯角は等しいので、
∠FEB = ∠DBC = 68°
弧CDの円周角より、
∠DBC = ∠CAD = 68°
CA = CDより、CADは二等辺三角形であり、その底角は等しいので、
∠CAD = ∠CDA = 68°
したがって、∠ACD（図中の⚫︎）は、
∠ACD = 180° – 68° × 2 = 44°
弧ADの円周角より、
∠ACD = ∠ABD = 44°
線分APは円Oの半径なので、
∠ABP = 90°
よって、∠DBP は、
∠DBP = ∠ABP – ∠ABD = 90° – 44° = 46°
中心角∠PODは、円周角∠DBPの2倍の大きさになるので、
∠POD = 2 × ∠DBP = 2 × 46° = 92°
したがって、おうぎ形OPDの弧DPの長さは、
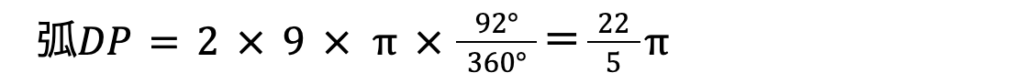
となります。
(2)の配点
配点 3点
大問7 総括
大問7では、図形の証明の問題が出題されました。
2025年度では、例年通りの円に内接する三角形の相似の証明の問題が出題されました。
(1)では、頂角の等しい2つの二等辺三角形があり、その底角が等しいことに気が付くことができるかどうか、がポイントでした。
証明内容の記述も長く、時間との勝負にもなった方もいらっしゃったのではないでしょうか。
(2)では、おうぎ形の中心角を使った弧の長さ計算が出題されました。
補助線を引いて、中心角を作成することがポイントとなります。
図形の証明の問題は、配点が高く、点数に大きく影響する問題です。
証明問題の練習だけではなく、色々な図形のそれぞれが持っている特徴などをしっかりと把握する意識を持って、
その知識を証明で活かすことが重要となります。
色々なパターンの問題にチャレンジして、応用力を磨いておきましょう。
個別学習Roots.について
個別学習Roots.は、
JR静岡駅の南口から徒歩3分の場所にある、個別指導＆個別学習教室
です。
学習の個別最適化を行い、効率的な学習を実践する教室です。
もし、今の自分を変えたい、もっと勉強に取り組みたいとお考えならば、ぜひ体験授業にお越しください。
生徒が落ち着いて勉強に集中しやすい環境を目指した教室は、シックで静かな雰囲気であるのも特徴です。
無料の個別教室説明会も随時開催していますので、お気軽にご相談ください。
<お問い合わせ先>
電話番号：080-7855-5240
メールアドレス：info@roots-kobetsugakusyu.com
住所：〒422-8061
静岡市駿河区森下町1-39 SOZOSYA森下町ビル2A