こんにちは!
JR静岡駅徒歩3分の中学生専門教室の個別学習Roots.(ルーツ)です。
このコラムでは、2025年度の静岡県公立高校入試問題の数学の解説を行います。
このような方は必見です!
- 2025年度に受験生になる新中学3年生
- 受験勉強のやり方が分からない中学生
- 過去問演習を行なっている受験生
また、個別学習Roots.では、個別の勉強相談を随時承っております。
ご興味のある方は、お気軽にお問い合わせください。
大問2 小問集合


(1) 作図
作図の問題では、
問題文に書かれている2つの条件にあった点を作図する問題
が頻出です。
問題文の条件に沿った直線を2本を作図して、
その交点が答えとなることが多い
です。
2025年度の問題では、条件が明記されていて出題されました。
この問題の作図の条件は、下記の2つです。
- 条件①:円の中心Oは、2辺BC, ACから等しい距離にあること。
- 条件②:円Oは、2点A, Cを通ること。
この条件に従って、作図を進めていきます。
条件①:角の二等分線の作図
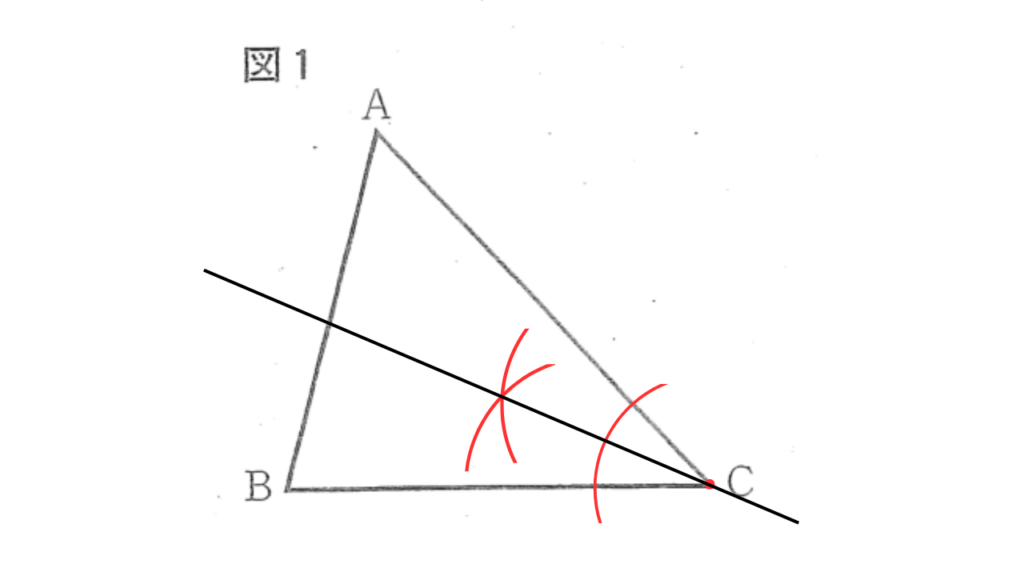
2辺BC, ACから等しい距離にある点は、∠Cの二等分線上の点となります。
上図の手順で、∠Cの二等分線を作図します。
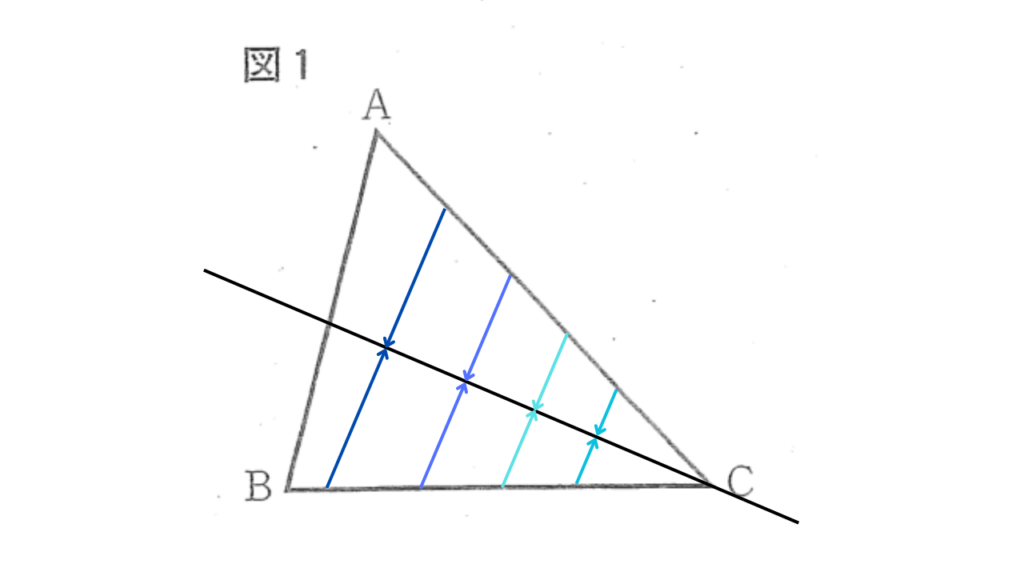
上図のように、∠Cの二等分線上の点はどこを取っても2辺BC, ACからの距離は等しいことが分かります。
条件②:垂直二等分線の作図
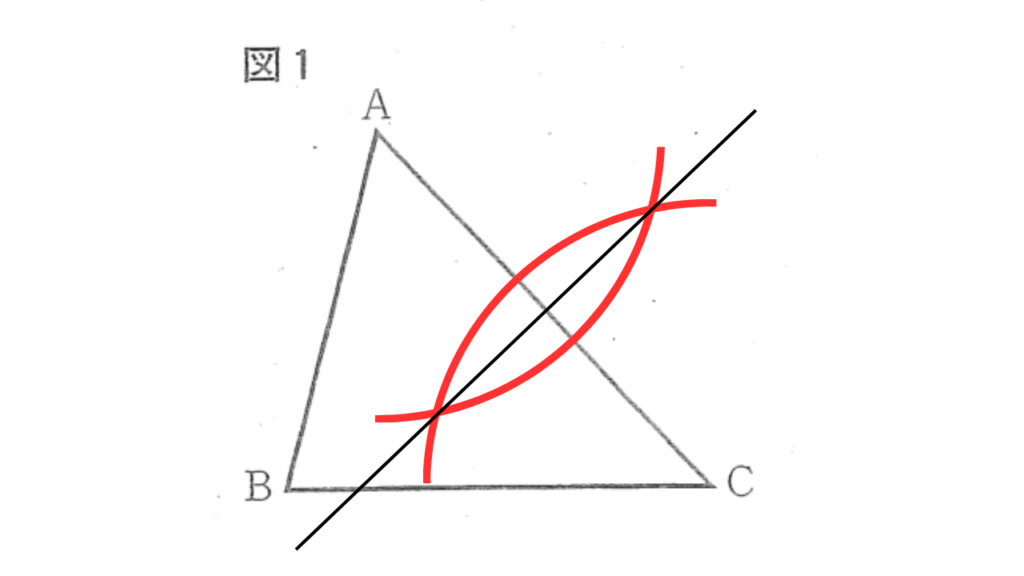
円Oは、2点A, Cを通るので、円の中心Oは、線分ACの垂直二等分線上にあることが分かります。
上図の手順で、線分ACの垂直二等分線を作図します。
(1) 作図の解答
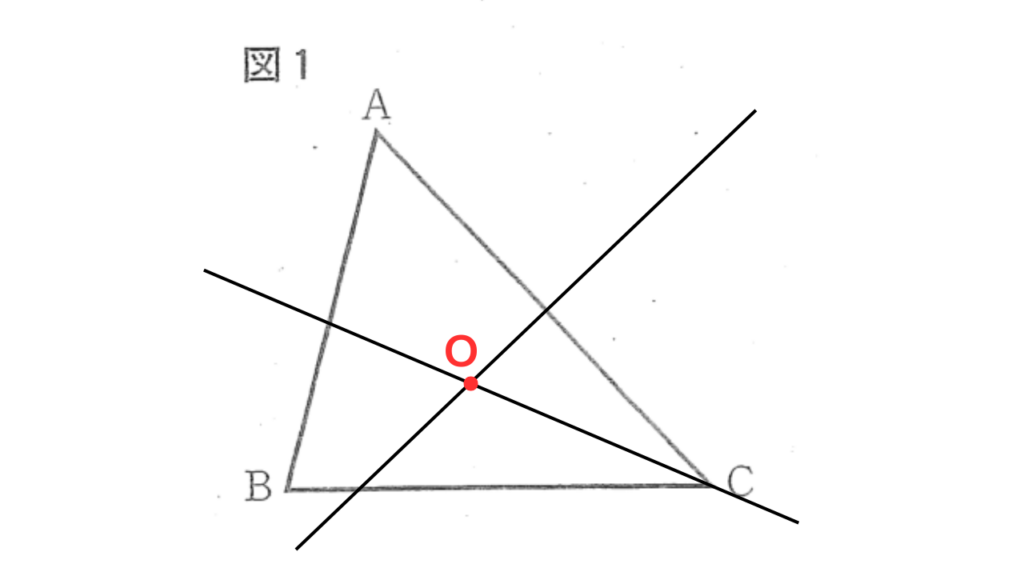
条件①と条件②で作図した直線の交点が点Oとります。
コンパスで描いた作図の跡は、消さずにのことしておきましょう。
また、作図が完了していても、「O」の記載を忘れてしまうと点数はもらえません。
必ず点Oを明確に記入しておきましょう。
(1)の配点
配点 2点
(2) 比例・反比例の式
(2)は、2つの数値の関係性を見付けて、式で表す問題です。
問題文から、水槽の容量である90 Lは変化しない定数であることが読み取れます。
また、毎分水を入れる量のx Lを増やすと、満水になるまでにかかる時間が減少する関係であることが分かります。
xとyの関係をまとめたものが、下記の表になります。

xの値が2倍、3倍、4倍…になると、yの値が1/2倍、1/3倍、1/4倍になっていることが読み取れます。
したがって、このxとyは、反比例の関係であることが分かります。
反比例の一般式は、

です。
また、上記の表から、xとyの積が必ず90に一定となることから、比例定数は90です。
よって、yをxの式で表すと、

となります。
(2)の配点
配点 2点
(3) 確率
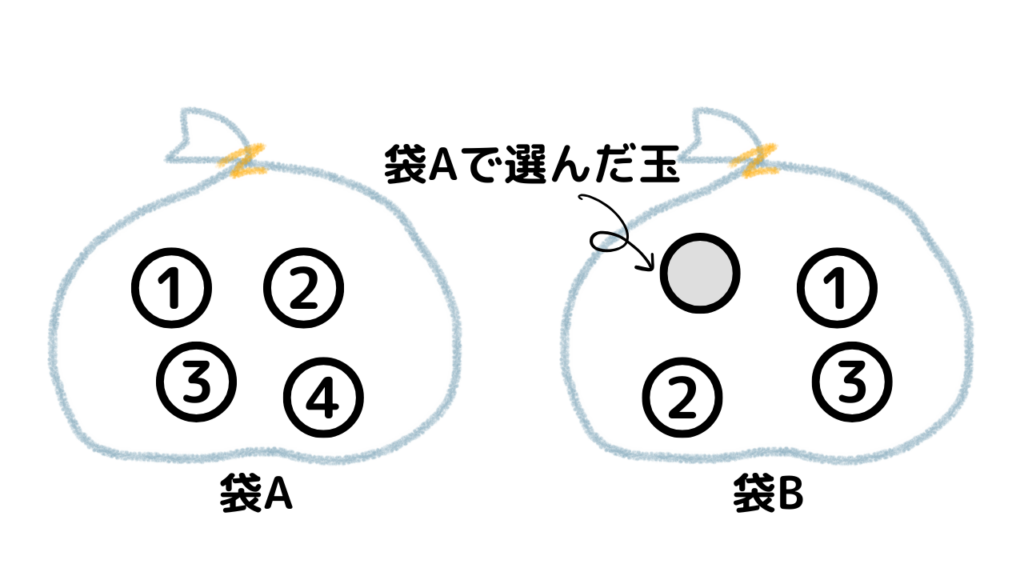
上記の図ように、袋Aと袋Bの両方に4つの玉が入っているもととして考えます。
下記の図は、袋Aから1個の玉を取り出して、その玉を袋B入れてから1個の玉を取り出すときの取り出し方を表した樹形図です。
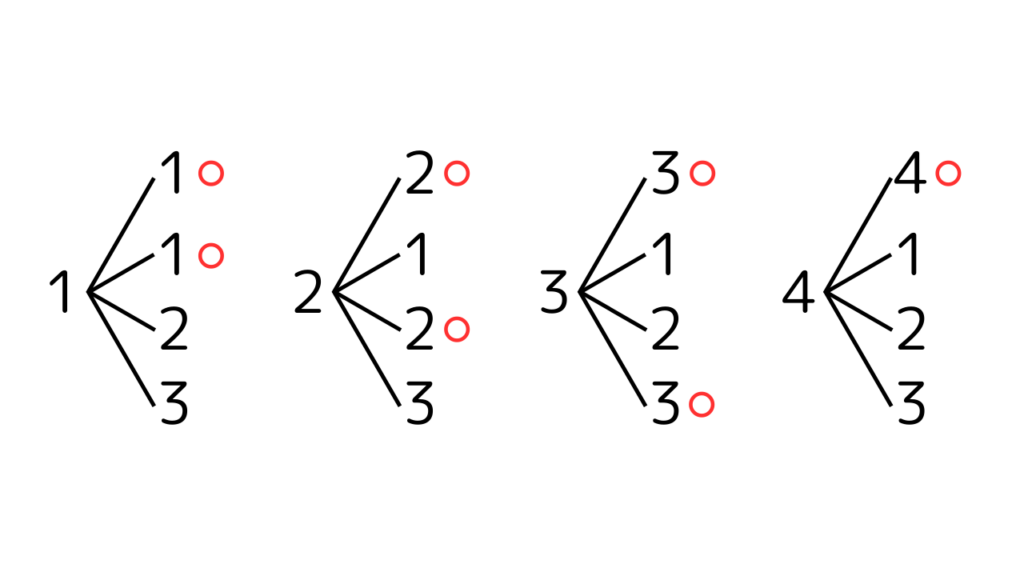
上記の樹形図より、
玉を取り出す組み合わせの総数は16通り、
袋Aと袋Bの両方から同じ数字を取り出す組み合わせ(赤い⚪︎)の総数は7通り
です。
したがって、解答は、

となります。
(3)の配点
配点 2点
大問2 総括

大問2の小問集合では、作図と関数と式、確率の問題が出題されました。
いずれの問題も例年通りの出題となりました。
大問1に比べて、単純な計算ではなく、数学的な思考力が問われる問題が設定されています。
しかしながら、いずれも教科書や学校のワークに掲載されている基本問題であり、正解しておきたい問題です。
配点も合計6点と高いく、大問1と合わせると18点も配点があります。
数学の基礎点となる問題ですので、しっかりと全問正解できるよう練習をしておきましょう。
日々の学習の中で、
ケアレスミスをしなくなるまで練習する、
という意識を持ってしっかりと点数に繋げていきましょう。
個別学習Roots.について

個別学習Roots.は、
JR静岡駅の南口から徒歩3分の場所にある、個別指導&個別学習教室
です。
学習の個別最適化を行い、効率的な学習を実践する教室です。
もし、今の自分を変えたい、もっと勉強に取り組みたいとお考えならば、ぜひ体験授業にお越しください。
生徒が落ち着いて勉強に集中しやすい環境を目指した教室は、シックで静かな雰囲気であるのも特徴です。
無料の個別教室説明会も随時開催していますので、お気軽にご相談ください。
<お問い合わせ先>
電話番号:080-7855-5240
メールアドレス:info@roots-kobetsugakusyu.com
住所:〒422-8061
静岡市駿河区森下町1-39 SOZOSYA森下町ビル2A



