【大問6：関数と図形】2025年度静岡県公立高校入試解説

こんにちは！
JR静岡駅徒歩3分の中学生専門教室の個別学習Roots.（ルーツ）です。

このコラムでは、2025年度の静岡県公立高校入試問題の数学の解説を行います。

また、個別学習Roots.では、個別の勉強相談を随時承っております。

ご興味のある方は、お気軽にお問い合わせください。

大問6 関数と図形

関数の問題を解く準備

静岡県の公立高校入試の問題や学力調査テストの関数の問題では、グラフが一緒に掲載されています。

しかしながら、問題文に書かれている点の座標やグラフの式といった情報はそのグラフ内に記載されていません。

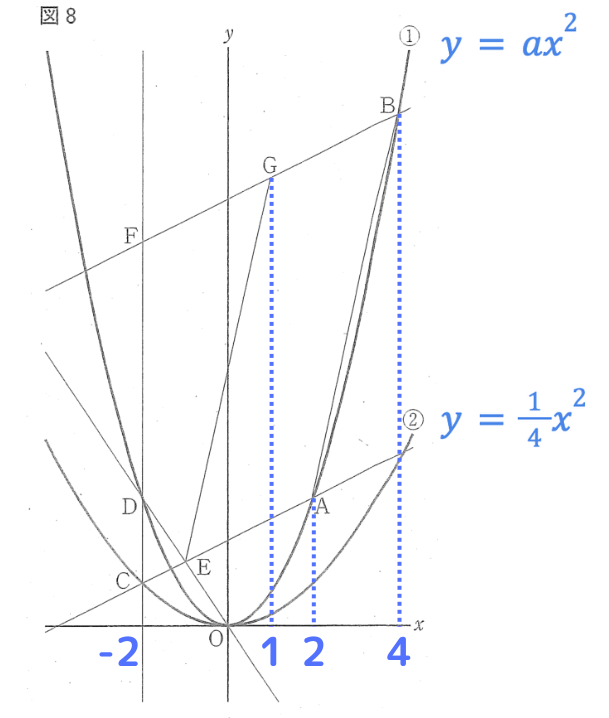
問題文の情報を整理すると同時に、一目で点の座標やグラフの式が読み取れることができるようにするためにも、下記のように問題文の情報はグラフにも書き込んで、問題を解く準備を必ずしておきましょう。

この作業をすることで、問題を解くのに掛かる時間を短縮やケアレスミス対策、問題の解き方の発想にも繋がります。
計算過程で出てきた数値も入力するようにしましょう。

(1) 定義域と値域

②のグラフは２次関数であり、傾きが0よりも大きいので、上に開いた放物線（下に凸）になります。
このグラフは、x=0で最小値をとり、左右対称の性質を持ちます。

より、最小値はx=0のときのy=0となります。

最大値は、原点から遠い端点のy座標となります。
与えられた範囲であるx=−2とx=3では、x=3が最も原点から遠い端点になるため最大値をとります。

したがって、yの変域は、

となります。

(1)の配点

配点　2点

(2)ア 直線の傾き

直線OAは、原点を通る比例のグラフです。

点Aのx座標は2であり、①のグラフが通るので、

となり、点Aの座標は、（ 2 , 4a ）と表すことができます。

比例のグラフの傾きは、xの値とyの値の商になるので、

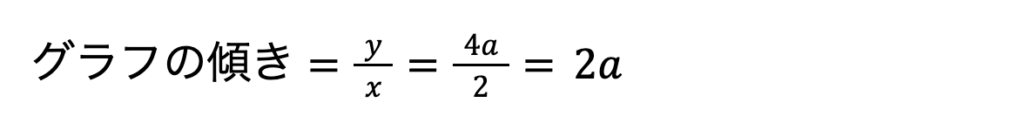
となります。

(2)アの配点

配点　3点

(2)イ 関数と図形

四角形GEABが平行四辺形になると仮定されているので、この条件を使ってaの値を考えていきます。

平行四辺形は対辺が平行であり、直線ACと直線BGも平行になるため、グラフの傾きが等しくなります。
直線ACと直線BGの傾きを計算して、aの値を求めます。

各点の座標

直線ACと直線BGの傾きを計算するために必要な点Aと点B、点C、点Gの座標を求めます。

◉ 点Aの座標
点Aの座標は、(2)アの計算過程より、（ 2 , 4a ）です。

◉ 点Bの座標
点Bの座標は、x座標が 4 であり、①のグラフが通るので、

となり、点Aの座標は、（ 4 , 16a ）と表すことができます。

◉ 点Cの座標
点Cの座標は、x座標が-2であり、②のグラフが通るので、

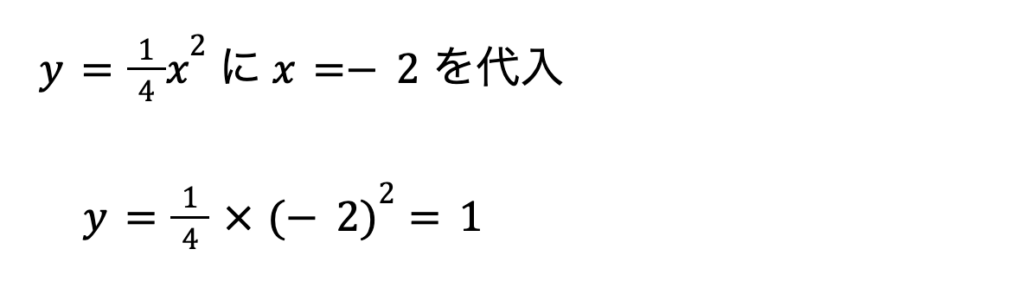
となり、点Cの座標は、（ -2 , 1 ）と表すことができます。

◉ 点Gの座標
点Gの座標を求めるために、点Eの座標から考えます。

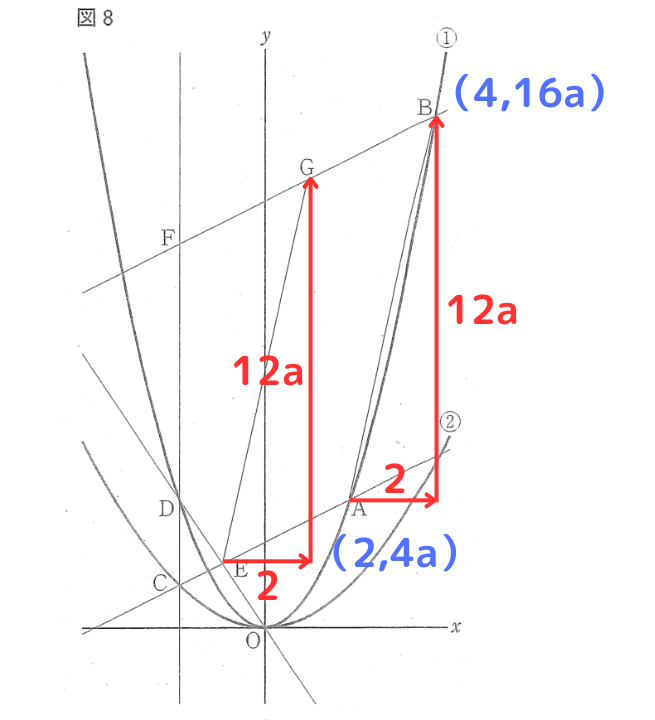
上図のように、点Bは点Aから、x軸方向に2、y軸方向に12aだけ移動させた点であることが読み取れます。

四角形GEABは平行四辺形なので、点Eと点Gでも同様に移動させることで座標を考えることができます。

点Gのx座標は1なので、点Eのx座標は-1であることが分かります。

点Eのx座標が1、点DのX座標が2なので、点Eは線分ODの中点ということが読み取れます。
よって、点Eのy座標は2aになり、点Eの座標は（ -1 , 2a ）となります。

点Eの座標からx軸方向に2、y軸方向に12aだけ移動させた点が点Gなので、点Gの座標は（ 1 , 14a ）になります。

直線ACと直線BGの傾き

次に、直線ACと直線BGの傾きを使ってaの値を計算します。

直線の傾きは、変化の割合と同じ値なので、

で計算することができます。

直線ACの傾きと直線BGの傾きは等しいので、

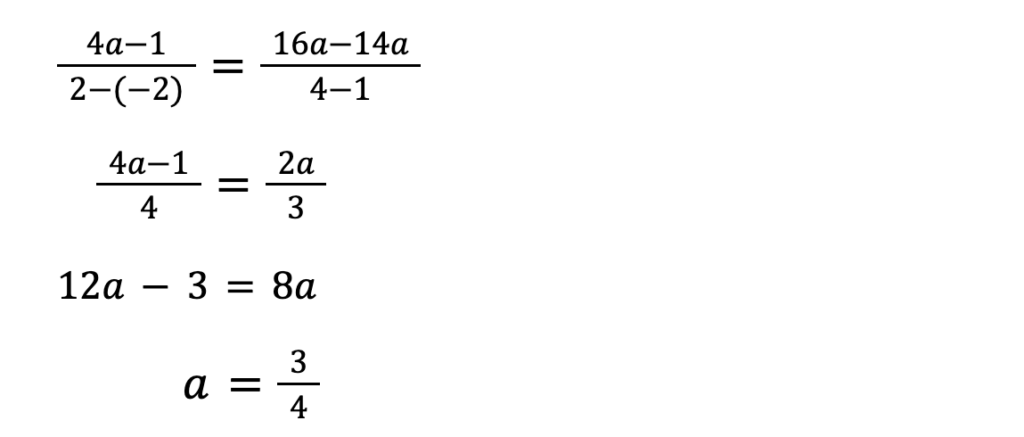
となります。

(3)イの配点

配点　3点

大問6 総括

大問6では、例年通り関数と図形の問題が合計8点配点で出題されました。

タブレット型端末を使ってグラフを変化させる形式の問題もここ数年で定番になってきており、
見覚えがあると感じた方もいらっしゃったかと思います。

(2)イの関数と図形が混ざった問題では、
平行四辺形の特性を活かした解き方を思いつく必要がありました。
平行四辺形に限らず、
色々な図形でのパターンをしっかりと把握しておくことが重要です。

前述しておりますが、
公立高校入試の問題や学力調査テストの関数の問題では、
掲載されているグラフに問題文に書かれている点の座標やグラフの式といった情報を書き込んで、
問題を解く準備をすることを習慣にしておきましょう。

情報を整理して、
求めることができるものを探して、
それを切り口に正解まで導いていきましょう。

個別学習Roots.について

個別学習Roots.は、
JR静岡駅の南口から徒歩3分の場所にある、個別指導＆個別学習教室
です。

学習の個別最適化を行い、効率的な学習を実践する教室です。

もし、今の自分を変えたい、もっと勉強に取り組みたいとお考えならば、ぜひ体験授業にお越しください。
生徒が落ち着いて勉強に集中しやすい環境を目指した教室は、シックで静かな雰囲気であるのも特徴です。

無料の個別教室説明会も随時開催していますので、お気軽にご相談ください。

<お問い合わせ先>
電話番号：080-7855-5240
メールアドレス：info@roots-kobetsugakusyu.com
住所：〒422-8061
静岡市駿河区森下町1-39 SOZOSYA森下町ビル2A