← 前回：大問1 計算問題の解説

大問2 計算問題の設問

(1) 作図

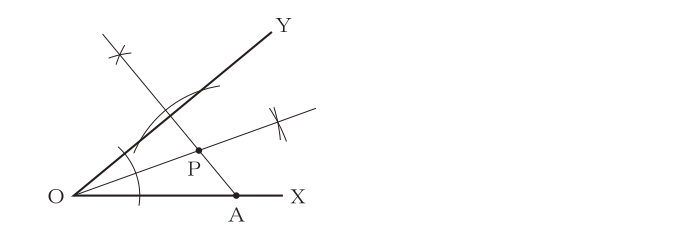
① 点Oを基準に∠YOXの二等分線を引きます。
② 点Aを基準に線分YOに対する垂線を引きます。
③ 引いた2本の直線の交点が点Pとなります。

  • ∠YOXの二等分線上の点は、2辺YOとXOから等しい距離にある点となることに気がつくことができるかが重要です。
  • 作図では、基本的に角の二等分線を応用する問題パターンが多いです。
  • 点Aを基準とした線分YOへの垂線の引き方を押さえておきましょう。

(1) 解答

配点　2点

(2) 文字式の利用

「aもbも正の数ならば、a + b は正の数である。」

の命題の逆は、

「a + b は正の数ならば、aもbも正の数である。」

となります。

a = -1 , b = 2 だった場合、a + b は正の数ではあるが、aもbも正の数ではないため、この命題は成立しません。

(2) 解答例

逆：a + b は正の数ならば、aもbも正の数である。

反例：a = -1 , b = 2

配点　2点（両方正しい回答で正解）

(3) 確率

取り出すカードの場合の数は、

4 × 5 = 20

で、20通りです。

袋Ⅱから取り出したカードに書いてある数が、袋Ⅰから取り出したカードに書いてある数の倍数になる組み合わせは、

( Ⅰ , Ⅱ ) = ( 2 , 4 ) , ( 2 , 6 ) , ( 2 , 8 ) , ( 3 , 6 ) , ( 3 , 9 ) , ( 4 , 8 ) , ( 5 , 10 )

の7通りです。

(3) 解答

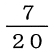
配点　2点

大問2 総括

大問2の小問集合では、作図と文字式の利用、確率の基本的な問題が出題されました。

大問1に比べて、単純な計算ではなく、数学的な思考力が問われる問題が設定されています。

いずれも基本的な問題で、配点も合計6点と高いので、しっかりと全問正解いしておきたい問題です。

大問2の想定時間配分は5分です。

しっかりと練習をしておきましょう。

続き：大問3 データの活用の解説 →

個別学習Roots.について

『個別学習Roots.』は、JR静岡駅の南口から徒歩3分の場所にある、個別指導＆個別学習教室です。

全ての生徒さんと毎週お話しをしながら、学習計画を作成して、継続的な学習ができる習慣作りのサポートをしております。
テスト対策や受験対策のご相談も承っています。

もし、今の自分を変えたい、もっと勉強に取り組みたいとお考えならば、ぜひ体験授業にお越しください。
自分を変えるにはあなた自身が変わろうと思い行動するほかありません。

教室は生徒が落ち着いて勉強に集中しやすい環境を目指した教室は、シックで静かな雰囲気であるのも特徴です。

<個別学習Roots.のお問い合わせ先>
● 電話番号：080-7855-5240 （担当：勝股）
● メールアドレス：info@roots-kobetsugakusyu.com
● 住所：〒422-8061　静岡市駿河区森下町1-39 SOZOSYA森下町ビル2A
● 教室のHPはこちらから！
● 公式LINEは↓のQRコードからお友だち登録をお願いします！

『個別学習Roots.』では、無料の教室説明会を開催しております。
無料説明会では、生徒の学習状況をヒアリングさせて頂いた上で、学習方法の提案まで行っております。

お気軽にお問い合わせください。