大問3 設問
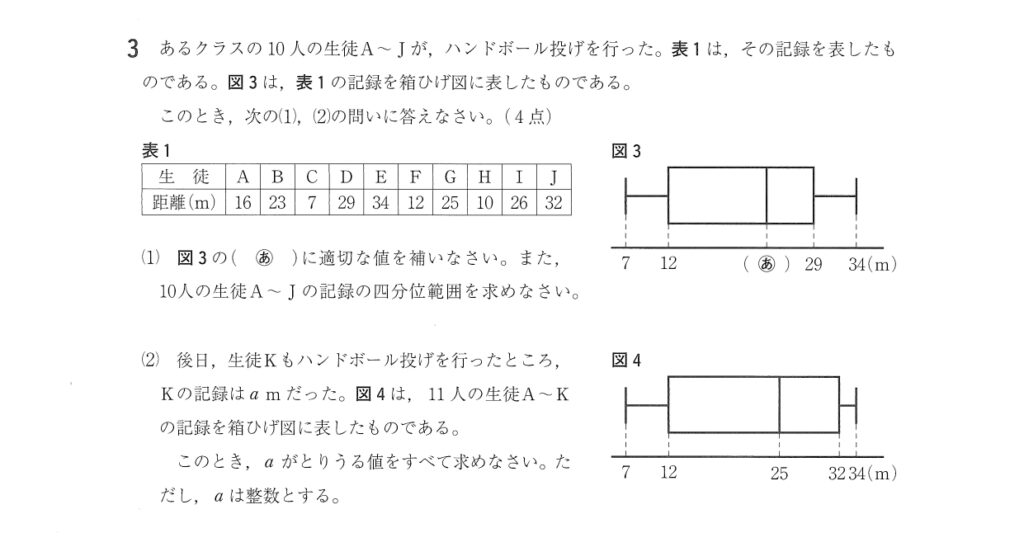
(1) 中央値(第2四分位数)と四分位範囲
箱ひげ図中の四角形の中の線は、データの中央値(第2四分位数)が該当します。
データを小さい順に並び替えて、真ん中の数値が中央値となります。
今回の問題のデータを小さい順に並べると、
7 , 10 , 12 , 16 , 23 , 25 , 26 , 29 , 32 , 34
となり、真ん中の数値は、23 と 25 になります。
データの数が偶数個で、真ん中の数値が2つある場合は、その2つの数値を足して2で割った数値が中央値となります。
中央値 = ( 23 + 25 ) ÷ 2 = 24
また、四分位範囲は、第1四分位数(データを小さい順に並べたときの下から1/4の数値)から第3四分位数データを小さい順に並べたときの下から3/4の数値)までの幅の広さになるので、第3四分位数と第1四分位数の数値の差で求めます。
四分位範囲 = 第3四分位数 – 第1四分位数 = 29 – 12 = 17
(1) 解答
あ 24
四分位範囲 17
配点 2点(両方正しい回答で正解)
(2) 箱ひげ図の比較
図3と図4の2つの箱ひげ図を比較して読み取れることは、
- 第1四分位数は変化していないが、第3四分位数が 29 から 32 に変わっていること
- 最大値の 34 は変わっていないこと
です。
したがって、生徒Kの記録は 32 ~ 34 mの範囲の数値であったことが読み取れます。
(2) 解答
32 , 33 , 34
配点 2点
参考:実際に箱ひげ図の利用されているデータ
「データがどの程度ばらついているか」を視覚的に捉えることができる箱ひげ図は、身近な場面であったり色々な記事で活用されています。
箱ひげ図を作成することで、平均値だけではわからないような傾向やデータの関係性・相関を見付けることに繋がります。
参考:色んな分布、箱ひげ図ひとつに(朝日新聞DIGITAL)
大問3 総括
大問3では、データの活用から箱ひげ図が出題されました。
2年生の数学の最後に習うこの単元は、学年末テストが終わった後の授業内容となることが多く、勉強に身が入らない学生が多くなりがちです。
箱ひげ図では、色々な用語はもちろんですが、それぞれがどの数値を表していて、どのような意味を持つかを理解しておきましょう。
また、箱ひげ図の問題でやりがちなケアレスミスは、数値を小さい順に並べ替えた際に、忘れてしまうデータが出てきてしまうことです。
数値を小さい順に並べ替えた後は、必ずデータの個数が合っているかの確認をしましょう。
データを扱う問題は高校入試問題はもちろんですが、静岡県学力調査テストにも頻出ですので、箱ひげ図やヒストグラムなどはしっかりと押さえておきましょう。
個別学習Roots.について

『個別学習Roots.』は、JR静岡駅の南口から徒歩3分の場所にある、個別指導&個別学習教室です。
全ての生徒さんと毎週お話しをしながら、学習計画を作成して、継続的な学習ができる習慣作りのサポートをしております。
テスト対策や受験対策のご相談も承っています。
もし、今の自分を変えたい、もっと勉強に取り組みたいとお考えならば、ぜひ体験授業にお越しください。
自分を変えるにはあなた自身が変わろうと思い行動するほかありません。
教室は生徒が落ち着いて勉強に集中しやすい環境を目指した教室は、シックで静かな雰囲気であるのも特徴です。
<個別学習Roots.のお問い合わせ先>
● 電話番号:080-7855-5240 (担当:勝股)
● メールアドレス:info@roots-kobetsugakusyu.com
● 住所:〒422-8061 静岡市駿河区森下町1-39 SOZOSYA森下町ビル2A
● 教室のHPはこちらから!
● 公式LINEは↓のQRコードからお友だち登録をお願いします!

『個別学習Roots.』では、無料の教室説明会を開催しております。
無料説明会では、生徒の学習状況をヒアリングさせて頂いた上で、学習方法の提案まで行っております。
お気軽にお問い合わせください。




2件のコメント
2件のピンバック