大問4 空間図形
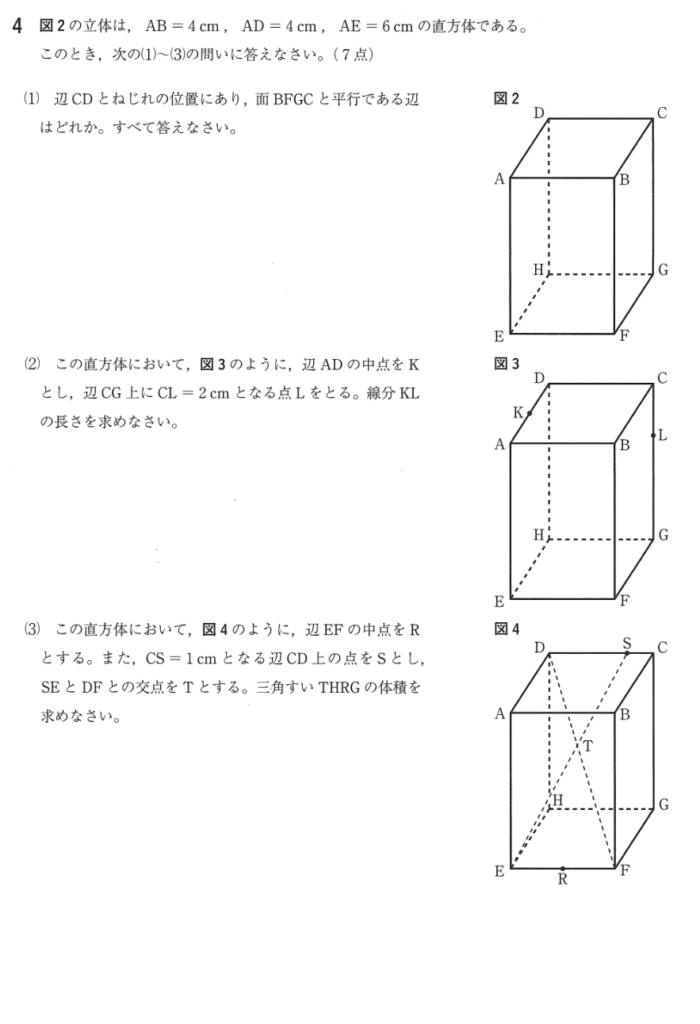
(1) ねじれの位置と平行
ねじれの位置にある2つの辺とは、交わってもいないし平行でもない辺の組み合わせです。
図2より、辺CDとねじれの位置にある辺は、
辺AE,辺BF,辺EH,辺FG
の4つです。
この中で、面BFGCと平行なものは、
辺AE,辺EH
です。
(1)の配点
配点 2点
(2) 三平方の定理と線分の長さ
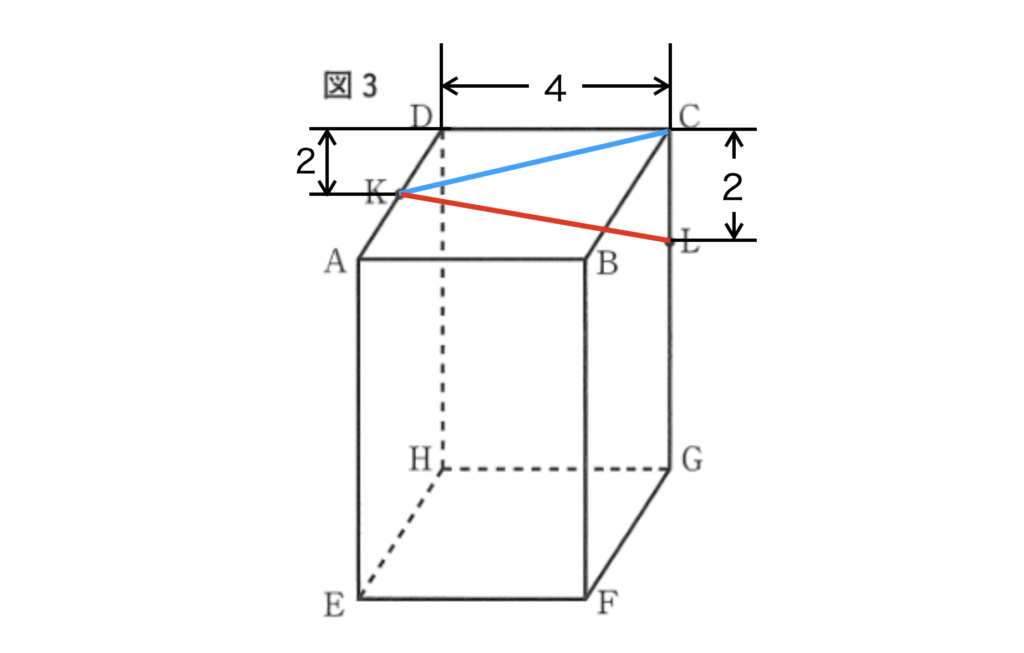
上図のように、線分KL(赤線)は、直角三角形KCLで三平方の定理を使って求めます。
直角三角形KCLにおいて、CLの長さは「2」なので、KCの長さを求める必要があります。
まずは、直角三角形KDCで三平方の定理を使ってKCの長さ(青線)から計算します。

上図より、KCの長さは、
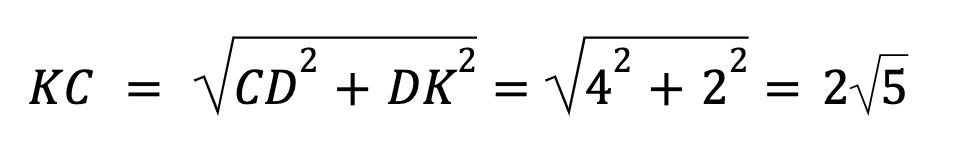
となります。
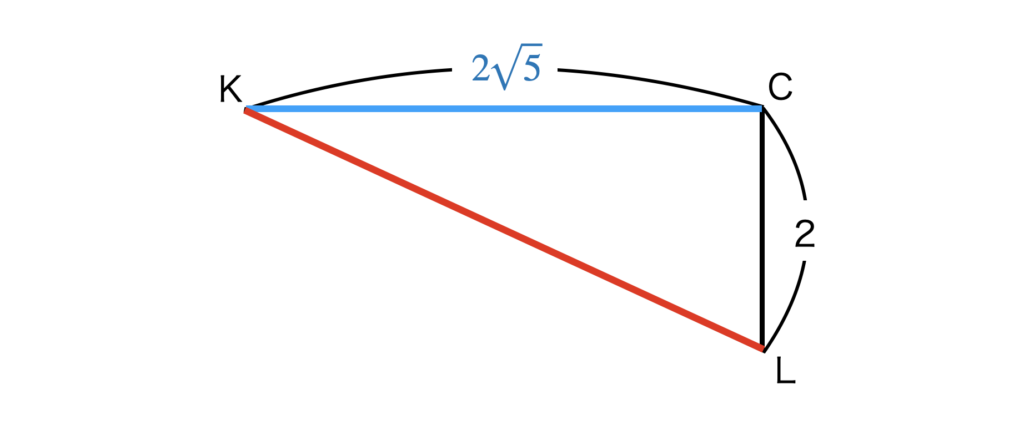
また、上図より、KLの長さは、

です。
(2)の配点
配点 2点
(3) 三角錐の体積
三角錐の体積の計算には、底面積と高さが必要です。
それぞれを計算して求めていきます。
三角錐の底面積の計算

上図のように、三角錐THRGの底面は、△HGRであり、その面積は、
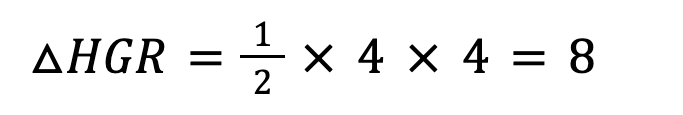
となります。
三角錐の高さの計算

上図のように、点Tから面HEFGに垂直に補助線を引いて、交点をJとしたとき、三角錐THRGの高さはTJになります。
また、同様に点Sからも垂線を引いてHGとの交点をIとしたとき、△ETJと△ESIは相似な関係となります。
この段階で、△ETJと△ESIとの相似比を使ってTJの長さを求めることができそうであると予想できます。
△ETJと△ESIとの相似比を求めるために、△TEFと△TSDに着目します。
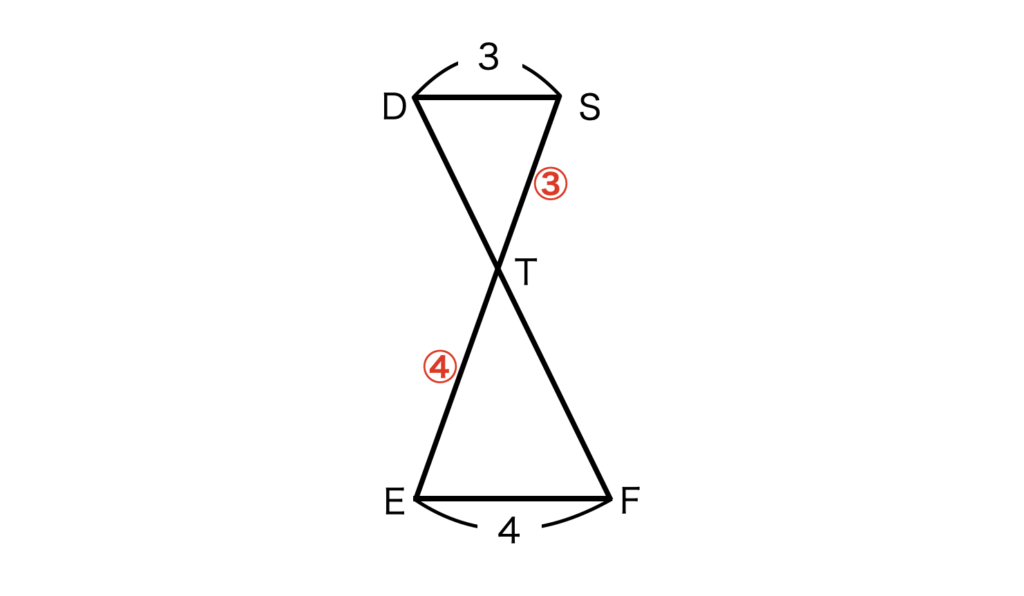
△TEFと△TSDも相似な関係(DS//FEより、2つの錯角が等しいため)であり、DS = 3 、FE = 4 より、相似比は△TEF:△TSD = 3:4 です。
したがって、ST:ET = 3:4 となります。
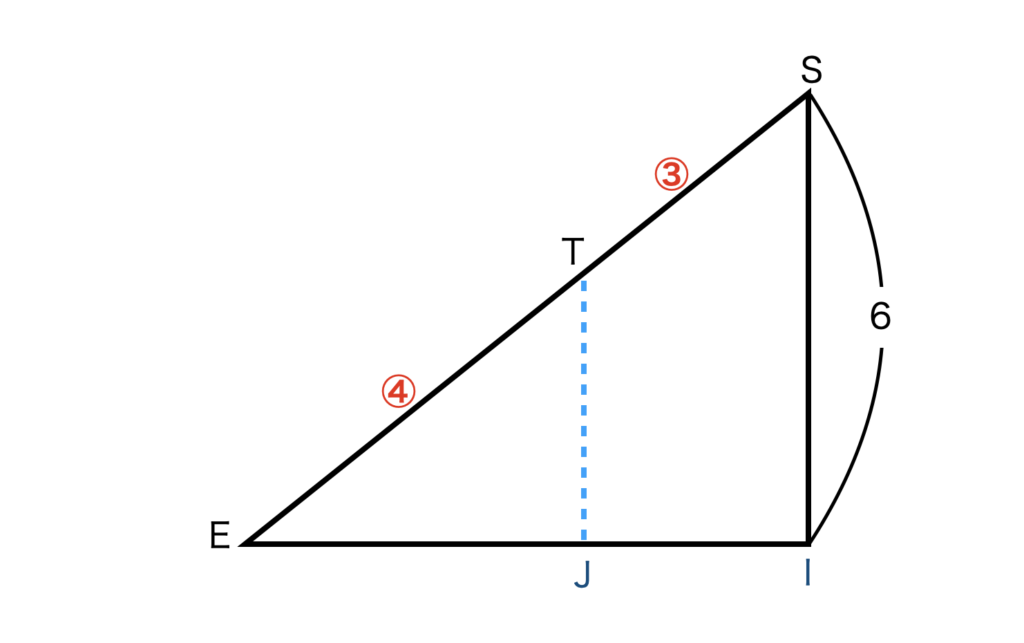
△ETJと△ESIとの図形にST:ET = 3:4 を考慮すると上図のようになります。
ST:ET = 3:4 より、ET:ES = 4:7 になるため、△ETJと△ESIの相似比は、△ETJ:△ESI = 4:7 となります。
この相似比を使って、TJの長さを求めると、
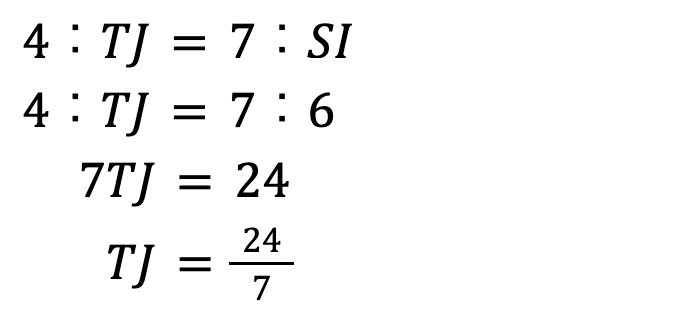
となります。
三角錐の体積の計算
したがって、三角錐THRGの体積は、
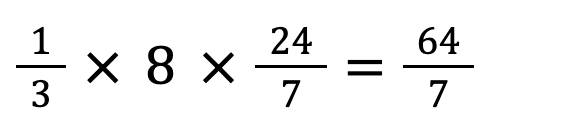
となります。
(3)の配点
配点 3点
大問4 総括
今年の空間図形の問題では、三角錐の体積の問題が出題されました。
三角錐の体積の計算では、その三角錐の底面積と高さが必要であり、それぞれをしっかりと計算することが求められます。
昨年度の空間図形よりも分かりやすい問題だった分、正解率も上がっていると予想されますので、偏差値が上位の高校を受験する方は、正解しておきたい問題でした。
空間図形の問題では、相似比や三平方の定理を駆使して、必要な辺の長さを求めるパターンが多いです。
まずは、問題の図の中で相似な図形を見つけて、与えられた情報の中から、どの辺の長さなら求めることができるかを整理して、答えに近づいていきましょう。
また、教科書で見たことがあるような、相似な図形の組み合わせに落とし込んで考えていくことも有効です。
今回の問題のように、なんとなく教科書の相似のページで見たことがある図形を探してそこから解き方の糸口を探していくこともテクニックの一つです。
静岡県の公立高校入試問題では、毎年必ず空間図形の問題は出題されます。
上記のテクニックや考え方のプロセスは練習しておきましょう。
個別学習Roots.について

『個別学習Roots.』は、JR静岡駅の南口から徒歩3分の場所にある、個別指導&個別学習教室です。
全ての生徒さんと毎週お話しをしながら、学習計画を作成して、継続的な学習ができる習慣作りのサポートをしております。
もし、今の自分を変えたい、もっと勉強に取り組みたいとお考えならば、ぜひ体験授業にお越しください。
自分を変えるにはあなた自身が変わろうと思い行動するほかありません。
教室は生徒が落ち着いて勉強に集中しやすい環境を目指した教室は、シックで静かな雰囲気であるのも特徴です。
<個別学習Roots.のお問い合わせ先>
● 電話番号:080-7855-5240 (担当:勝股)
● メールアドレス:info@roots-kobetsugakusyu.com
● 住所:〒422-8061 静岡市駿河区森下町1-39 SOZOSYA森下町ビル2A
● 教室のHPはこちらから!
● 公式LINEは↓のQRコードからお友だち登録をお願いします!

『個別学習Roots.』では、無料の教室説明会を開催しております。
無料説明会では、生徒の学習状況をヒアリングさせて頂いた上で、学習方法の提案まで行っております。
お気軽にお問い合わせください。




2件のコメント
2件のピンバック